星期三, 21. 十二月 2016 07:57下午
卡尔曼滤波是一种高效率的递归滤波器(自回归滤波器),它能够从一系列的不完全及包含噪声的测量中,估计动态系统的状态。
卡尔曼滤波简介
卡尔曼滤波的一个典型实例是从一组有限的,包含噪声的,通过对物体位置的观察序列(可能有偏差)预测出物体的位置的坐标及速度。在很多工程应用(如雷达、计算机视觉)中都可以找到它的身影。同时,卡尔曼滤波也是控制理论以及控制系统工程中的一个重要课题。例如,对于雷达来说,人们感兴趣的是其能够跟踪目标。但目标的位置、速度、加速度的测量值往往在任何时候都有噪声。卡尔曼滤波利用目标的动态信息,设法去掉噪声的影响,得到一个关于目标位置的好的估计。这个估计可以是对当前目标位置的估计(滤波),也可以是对于将来位置的估计(预测),也可以是对过去位置的估计(插值或平滑)。这种滤波方法以它的发明者鲁道夫.E.卡尔曼(Rudolph E. Kalman)命名,原文地址 。
卡尔曼滤波是一种递归的估计,即只要获知上一时刻状态的估计值以及当前状态的观测值就可以计算出当前状态的估计值,因此不需要记录观测或者估计的历史信息。卡尔曼滤波器与大多数滤波器不同之處,在於它是一种纯粹的时域滤波器,它不需要像低通滤波器等频域滤波器那样,需要在频域设计再转换到时域实现。
初识卡尔曼滤波
先举个简单例子说明卡尔曼滤波干嘛的,下面有三幅图,第一幅是原图,小车匀速前行,第二幅的时候可以预测出当前位置,但是越往后随着各种误差会很难判断出小车的位置了,假如我们有一个新加入的量,比如一个雷达用来探测小车位置,也就是有两种方法,误差小的时候没啥,误差大了的时候该怎么去判断小车在哪里,哪个的测量值更可靠,如何求得那个比例值,使其能够得出目前的位置。
初始小车行驶:
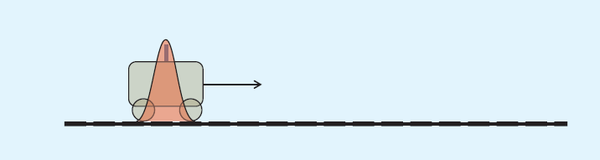
前进一段时间:

加入了另一种方式:
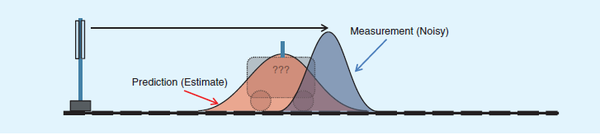
kalmanfilter方式:

数学公式介绍
下面是卡尔曼滤波算法的五大式:
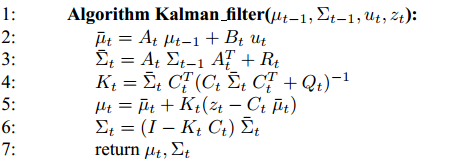
公式中详细的说明了滤波方法的步骤,主要如下(用的符号有点不同,意思一样): 首先给出一个控制理论中公式
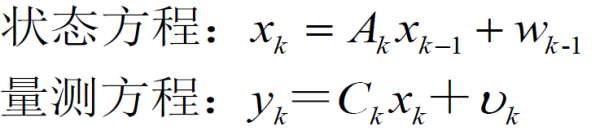
卡尔曼滤波就是利用状态过程噪声和测量噪声对状态进行估计。 一个状态在一个时刻点k的状态进入下一个时刻点k+1状态,会有很多外界因素的干扰,我们把干扰就叫做过程噪声,用w表示。任何一个测量仪器,都会有误差,我们把这个误差叫做量测噪声,用v表示。 回到上面那个公式,状态方程表示状态在不断的更新,从一个时刻点进入下一个时刻点,这个很好理解。关键是量测方程,它表示,我们不断更新的状态有几个能用测量仪器测出来,比如,汽车运动状态参数有很多,比如速度,轮速,滑移率等,但是我们只能测量出轮速,因此量测方程要做的就是把状态参数中能量测的状态拿出来。
演化过程
1.首先假定我们只有一个线性方程求取下一时刻的位置信息
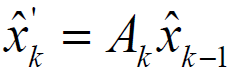
2.不考虑测量噪声取出能测量的状态,也很简单:
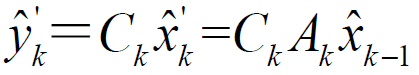
3.用测量仪器测量出来的状态值(大家可以考虑到:测量的值就是被各种噪声干扰后的真实值)减去上面不考虑噪声得到的测量值:
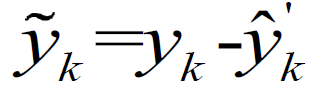
这个值在数学上是一个定义值,叫做新息,有很多有趣的性质,感兴趣的可以自己谷歌。 我们对步骤暂且停一停。这个叫新息的值有什么用?由上面的过程我们可以明显看到,它反映了过程噪声和测量噪声综合对测量状态值的影响,也就是它包含了w和v的情况。 一个数值c由两部分内容a和b组成,那么怎样用数学表达式来表达? 一般有两种做法: I.直接相加:c=a+b; II. 用比例的方法:a=n*c,b=(1-n)c 卡尔曼采用了方法II,用比例的方法来做(其实这也是为什么叫做滤波的原因,因为滤波就是给权值之类的操作)。也就是说,过程噪声w=新息一个比例。这样得到的过程噪声加上原来(第一步)不考虑过程噪声的状态值不就是优化值了吗? 也就是:
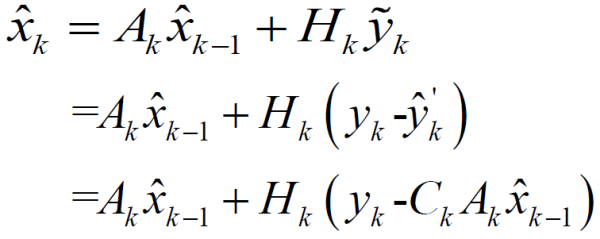
Okay,都写到这里了,有必要做一下前提假设: a. 什么高斯噪声,均值为零一堆; b.Ak,Ck,wk的协方差Q,vk的协方差R,系统协方差初始值P0,状态初始值X0,都已知。 那么到目前为止我们的思路就是清楚了,找到一个合适的Hk值(卡尔曼增益),那么我们就能得到状态的最优值。
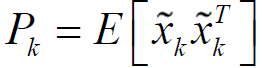
这是误差协方差矩阵。 思路:使得误差协方差矩阵Pk最小的Hk。 为什么?这里我从感观的角度说明自己的理解,欢迎讨论。 协方差表示什么,协方差表示两者之间的联系或者关系,关系越大,协方差越大。误差协方差越小说明过程噪声和量测噪声的关系越小。关系越小能做什么,这要回到我们第3步讨论的我们用比例的方法分开了w和v。用比例分开,到底多少属于w,多少是v,如果关系越小,分开的越精确,比如一堆白砂糖和盐,如果两种混合的很均匀,我们说它关系很大,也就越难用比例的方法将其分开。 4.求的误差协方差矩阵Pk
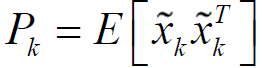
自然是把里面的Xk先得到,然后公式运算,通过上面的步骤我们也容易得到:
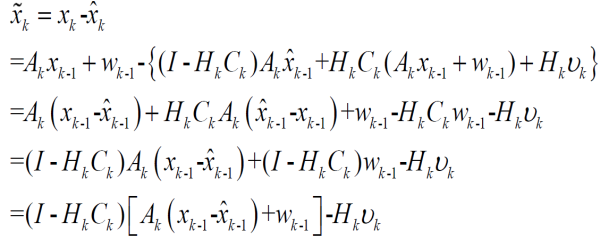
然后复杂的数学计算,和之前假设的高斯噪声,新息的性质之类,就能得到下面的卡尔曼滤波递推公式:
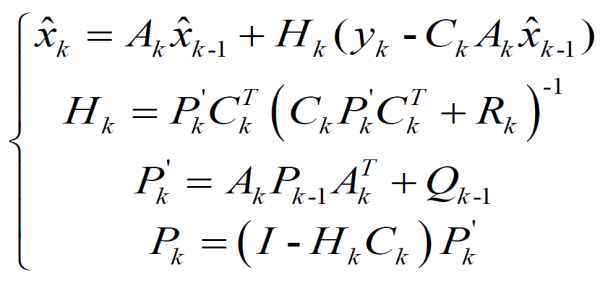
通过上面的解释,我们也就不难知道这些公式都在干嘛,知道干嘛就可以了。在知道A,C,P0,Q,R的情况下,整个公式的运算流程也都很清晰了。
Python下代码如下所示:
#coding=utf-8
import numpy
import pylab
#这里是假设A=1,H=1的情况
# 参数初始化
n_iter = 50
sz = (n_iter,) # size of array
x = -0.37727 # truth value (typo in example at top of p. 13 calls this z)真实值
z = numpy.random.normal(x,0.1,size=sz) # observations (normal about x, sigma=0.1)观测值
Q = 1e-5 # process variance
# 分配数组空间
xhat=numpy.zeros(sz) # a posteri estimate of x 滤波估计值
P=numpy.zeros(sz) # a posteri error estimate滤波估计协方差矩阵
xhatminus=numpy.zeros(sz) # a priori estimate of x 估计值
Pminus=numpy.zeros(sz) # a priori error estimate估计协方差矩阵
K=numpy.zeros(sz) # gain or blending factor卡尔曼增益
R = 0.1**2 # estimate of measurement variance, change to see effect
# intial guesses
xhat[0] = 0.0
P[0] = 1.0
for k in range(1,n_iter):
# 预测
xhatminus[k] = xhat[k-1] #X(k|k-1) = AX(k-1|k-1) + BU(k) + W(k),A=1,BU(k) = 0
Pminus[k] = P[k-1]+Q #P(k|k-1) = AP(k-1|k-1)A' + Q(k) ,A=1
# 更新
K[k] = Pminus[k]/( Pminus[k]+R ) #Kg(k)=P(k|k-1)H'/[HP(k|k-1)H' + R],H=1
xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k]) #X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)], H=1
P[k] = (1-K[k])*Pminus[k] #P(k|k) = (1 - Kg(k)H)P(k|k-1), H=1
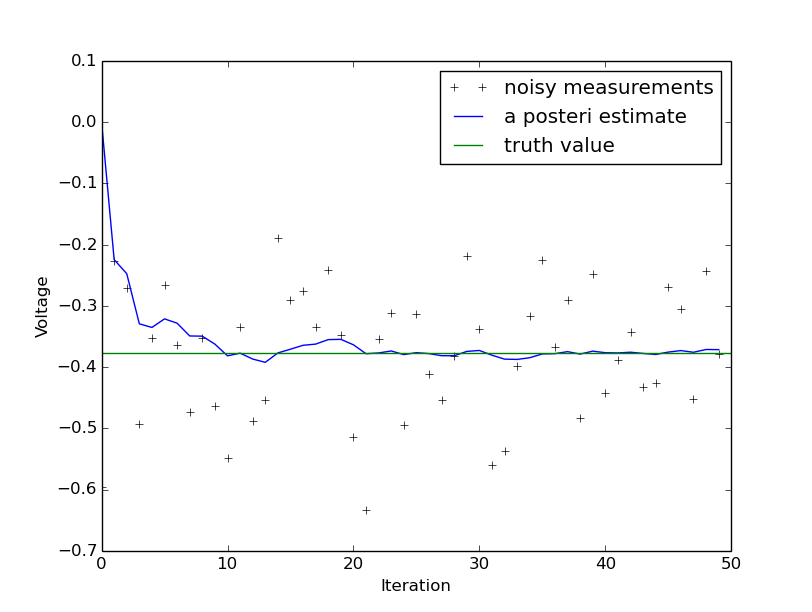
pylab.figure()
pylab.plot(z,'k+',label='noisy measurements') #观测值
pylab.plot(xhat,'b-',label='a posteri estimate') #滤波估计值
pylab.axhline(x,color='g',label='truth value') #真实值
pylab.legend()
pylab.xlabel('Iteration')
pylab.ylabel('Voltage')
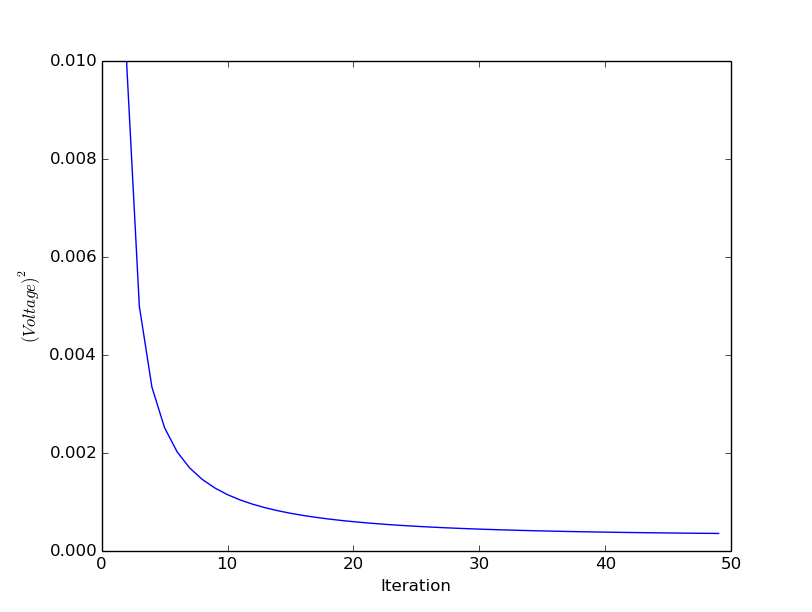
pylab.figure()
valid_iter = range(1,n_iter) # Pminus not valid at step 0
pylab.plot(valid_iter,Pminus[valid_iter],label='a priori error estimate')
pylab.xlabel('Iteration')
pylab.ylabel('$(Voltage)^2$')
pylab.setp(pylab.gca(),'ylim',[0,.01])
pylab.show()
截图如下:
文中链接:
卡尔曼滤波算法–核心公式推导导论:链接地址